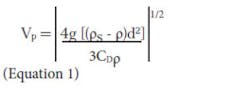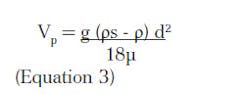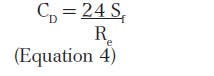This is part 2 of 4. The first article on gravity separation covers basic principles, and can be found here.
Determining Settling Velocities
Stormwater exhibits a distribution of settling velocities, a reflection of the complex mixture of solids of different sizes, shapes, specific gravities, and water temperatures. The settling velocity distribution is determined two ways. If the size distribution is known, the settling velocity distribution is calculated using Stokes Law and related equations. The second method is direct measurement of settling velocities. Each method has its advantages and disadvantages.
Stokes Law. Equation 1 describes the settling velocity of a spherical particle in quiescent water. The equation applies to spherical particles whether they are denser or lighter than water.
Where:
Vp = settling velocity of a particle
g = gravity constant
ρs = density (specific gravity) of particle
ρ = density (specific gravity) of water
d = particle diameter
CD = drag coefficient (dimensionless)
The drag coefficient (CD), related to the Reynolds Number (Re), describes the hydrodynamic condition of the fluid at the particle surface. As size increases the drag coefficient decreases. The relationship is shown in Figure 1 (see Part 1 of this series). Shown are the three hydrodynamic conditions: laminar, transition, and turbulent.
The fluid condition described in Equation 1 is not of the water, but of the fluid boundary surrounding the particle. In the laminar zone, viscous forces dominate with small particles because of their large surface area in relation to their volume. Drag decreases linearly with increasing particle size, as the surface area of the particle decreases relative to its volume. The relationship begins to deviate from linear as the settling velocity increases because inertial forces become significant. The transition area occurs where inertial forces gradually become more significant. Eventually, inertial forces dominate and a completely turbulent condition exists around the particle. In the turbulent condition drag does not change with increasing particle size.
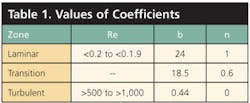
Equation 2, derived from Equation 1, describes the relationship between the Reynolds Number and the drag coefficient, as are values for constants b and n in Table 1. Demarcation points between the three hydrodynamic regimes are not distinct. Re is the Reynolds Number.
Stokes Law describes settling velocities only under laminar conditions. Recognizing that Re = ρVp d/µ and CD = 24/ Re for the laminar condition, Equation 1 modifies to give Stokes Law in Equation 3. The absolute viscosity is µ.
For the transition from laminar to turbulent, Stokes Law is not valid, and the values for b and n in Table 1 transform Equation 3 to Equation 4. The CD for the turbulent condition is constant at about 0.44. Equation 4 is revised to Equation 5. Both Equations 3 and 5 can be used with metric or English units. A conversion factor X is needed for Equation 4: 0.072 for metric units and 2.32 for Imperial units.
Equations 1 through 3 assume the settling particles are spherical. Non-spherical particles experience higher drag forces, resulting in a settling velocity that is lower than the calculations from Equations 1 through 3. Equation 4 incorporates the effects of particle shape on the drag force by using a shape factor, Sf.
For a smooth spherical particle, the value of Sf is 1. For sand or silt, it is 2. Thus, sand and silt have a settling velocity about half of a spherical particle. Fall velocities of uniform shapes other than spheres have been studied. There are no shape factors for organic solids or chemical flocs. Graphite flakes have a Sf of 22, suggesting organic solids likely have a shape factor greater than that of sand, but this has not been evaluated. Organic solids settle considerably slower than inorganic solids, as does clay, given their shape factors. The effect of temperature on settling velocities is significant for stormwater given the range experienced. As temperature decreases, settling velocities decrease due to the increase in the viscosity of water. The same occurs with saline stormwater due to deicing salts. A study found that the combination of saline water and low temperature reduced the settling by about half.
Clay appears to deviate significantly from Stokes Law at very low temperatures. Stokes Law states that the settling rate decreases with decreasing temperature due to increasing water viscosity. However, forces that inhibit flocculation are reduced with decreasing temperature. According to Stokes Law, the settling rate of clay should decrease by 45% with a temperature decrease from 25 to 5°C, yet it has been observed to increase by 30%.
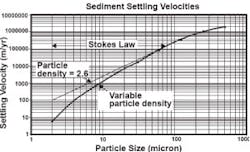
In contrast, a study of stormwater (Figure 2) found significant deviation from Equation 3, with the standard input of specific gravity at 2.65, beginning at about 20 microns (the upper line). The settling rate for 10 microns was only about 10% of that calculated with Equation 3. Figure 2 indicates the potential deviation of very small particles from the standard Stokes Law when a specific gravity of 2.6 is assumed for all particles. The deviation starts at 20 microns. It is often stated that settling in stormwater systems do not follow Stokes Law. This is not true. Deviations are found simply because shape factors and the inputs for specific gravity and temperature are wrong for the situation.
Even for the prediction based on a specific gravity of 1.5, common for some clays and organic matter, the lower portion of the middle line overstates the observed settling rates of particles in stormwater. The difference between the middle and lower lines might be due to shape, such as the clays and fine silts appearing as more or less flat plates. For example, micaceous clay flakes have settling rates two orders of magnitude lower than a sphere of the same specific gravity. The deviation gets greater as the particle size gets smaller, as indicated in Figure 2.
A review of over a dozen studies found that the specific gravity of individual studies ranged from 1.1 to 2.86, with most above 2. Only three of the studies cited had values in the range of 2.6, the most common specific gravity used to calculate settling rates of particles in stormwater. One study in which the sample was mostly organic had the density of 1.1. A significant portion of the sediment can be organic, 25 to 50% in a review of six studies. Mixes used in laboratory testing such as Sil-Co-Sil 106 behave differently than sediments in stormwater. Generally, better removal is expected in laboratory studies due to the absence of materials with specific gravities less than 2.6, assuming the same particle size distribution of laboratory and stormwater sediments.
As shown in Equations 1 through 5, particle size is required to calculate settling velocity. Particle sizes are typically determined through the use of standard soil sieve tests that commonly measure particles as small as 75 microns, although sieves as small as 25 microns have been used. Sizes of smaller particles are determined using the hydrometer procedure. This method gives settling velocities directly, from which the size distribution is calculated using a modified Stokes Law as specified. For others who may use these data to recalculate settling velocities, it is important to use the equation provided in the method. The equation specifies a coefficient shape factor of about 1.75. A common error in calculating settling rate of particle sizes is to leave out the shape factor, grossly overstating the settling velocity.
Further considerations make use of Equation 3 problematic. Drying and grinding of samples prior to sieving modifies the original size distribution. In the hydrometer test, dried material is wetted with distilled water, with a significantly different chemistry than stormwater. Therefore, the results do not represent the sediment sizes present in the original stormwater sample. It is suggested that samples not be dried prior to sieving, thereby avoiding the bias of rewetting. A comparison of dry and wet sieving of street sediment samples found that dry sieving understated the fraction of particles less than 75 microns by a factor of two. Wet procedures are available.
Editor’s note: This story on is continued here: “The Principles of Gravity Separation, Part 3“